 Estamos habituados a fazer previsões ou estimativas baseadas no crescimento de números como 1, 3, 5, 7, … (progressão aritmética), mas raramente pensamos em outras formas de crescimento, como 1, 2, 4, 8, 16, … (progressão geométrica).
Estamos habituados a fazer previsões ou estimativas baseadas no crescimento de números como 1, 3, 5, 7, … (progressão aritmética), mas raramente pensamos em outras formas de crescimento, como 1, 2, 4, 8, 16, … (progressão geométrica).
A nossa falta de prática neste segundo caso é desarmante: quando queremos usar a intuição para fazer previsões, as nossas expectativas falham estrondosamente.
Uma resma de folhas, daquelas que colocamos nas nossas impressoras de casa, tem cerca de 50 mm de espessura e contém 500 folhas, o que dá a espessura e=0,1 mm por cada folha.
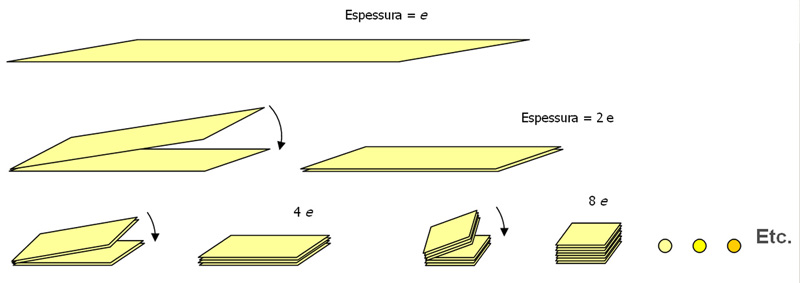
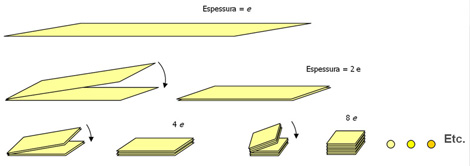
Imagine-se uma fita muito comprida, feita desse papel. Dobrando a fita ao meio pela primeira vez, teremos o dobro da espessura (2e=0,2 mm), como a figura mostra (veja a figura em grande no fim do artigo); dobrando novamente a fita, após a segunda dobragem a espessura do papel atingirá 0,4 mm, e assim sucessivamente.
O papel dobrado continua fino, diremos nós, seguros e confiantes, do alto da nossa experiência de vida. Por mais vezes que se dobre o papel, a espessura será sempre pequena, pensamos nós.
É claro que todos sabemos que, ao fim de algumas dobragens, será preciso uma força enorme para dobrar o papel, e seria necessário ter à partida uma tira de papel gigantesca para o poder dobrar sucessivamente.
Vamos desprezar esses factos e pensar no modo como cresce a espessura de papel, à medida que este vai sendo sucessivamente dobrado, pois o nosso interesse fundamental é ver como é que a espessura vai aumentando.
Quantas vezes seria preciso dobrar o papel para obter uma espessura igual à distância média da Terra à Lua (384 400 km)? Parece que teríamos de o fazer milhares de vezes, ou provavelmente milhões de vezes (o senso comum diz-nos isso), mas… ao fim de 42 dobragens a espessura do papel dobrado já excedeu essa distância.
Continuando a dobrar a fita de papel, à 51.ª dobragem (contada desde o início), já a espessura de papel excede 150 milhões de km, que é aproximadamente a distância média da Terra ao Sol.
Poucas dobragens depois, mais precisamente à 67.ª dobragem (contada desde o início), a espessura do papel excederia um ano-luz (1 ano luz=9,461 000 000 000 km). Isto representa 63 200 vezes a distância da Terra ao Sol.
À 83.ª dobragem (contada desde o início), a espessura do papel excede o diâmetro tradicionalmente considerado da nossa galáxia! (100 000 anos-luz). Quem diria?
Texto e figura de Guilherme de Almeida
Ciência na Imprensa Regional – Ciência Viva
Guilherme de Almeida nasceu em 1950. É licenciado em Física pela Faculdade de Ciências de Lisboa e foi professor desta disciplina, tendo incluído Astronomia na sua formação universitária.
Realizou mais de 80 palestras e comunicações sobre Astronomia, observações astronómicas e Física, em escolas, universidades e no Observatório Astronómico de Lisboa.
Utiliza telescópios, mas defende a primazia do conhecimento do céu a olho nu, antes da utilização de instrumentos de observação.
Escreveu mais de 90 artigos de Astronomia e Física. É autor de oito livros: Sistema Internacional de Unidades; Itens e Problemas de Física–Mecânica (co-autor); Introdução à Astronomia e às Observações Astronómicas (co-autor); Roteiro do Céu; Observar o Céu Profundo (co-autor); Telescópios; Galileu Galilei; O Céu nas Pontas dos Dedos. A obra Roteiro do Céu foi publicada em inglês, sob o título “Navigating the Night Sky (Springer Verlag–London). O livro Galileu Galilei também está publicado em castelhano e catalão.